Universal properties are virtual governors
Mathematical structures like the Cartesian product aren’t really defined by their elements but by a system-level preference embodied in the relationships among the members of the system—in other words, a virtual governor. The virtual governor’s job is to define the anatomical goals of the mathematical system and to serve as the means by which optimal solutions are identified.
The Cartesian product is characterized by a universal property. A universal property refers to an object that has the same kind of relationship with every other object in the system. For the Cartesian product, the system is the system of objects that could do the job of being the Cartesian product, and the object that does the job best is the one that the same kind of relationship—a universal relationship—with every other object in the system, including itself.
A simpler example is the concept of a maximum element in an ordered set. Suppose our set is S = {1, 2, 3} with 1 < 2 < 3 and 1 = 1; 2 = 2; 3 = 3. Then 3 is the maximum element because it is greater than or equal to every other element in the set. It also has the same singular relationship with every other object in the set: for all x in S, we have
All universal properties work this way: they are all examples of a maximum or minimum element in some context.
Universal properties are a good candidate for virtual governors for several reasons:
Universal properties define a group-level problem and constitute the means by which to identify the optimal group-level solution. The system of relationships that define the Cartesian product of sets A and B up to unique isomorphism identify both what the problem the members of the system are trying to accomplish—projecting to A and B efficiently—and what the test is for whether an object X is an efficient solution—the presence of the universal property relating all other candidates for an efficient solution to X. I.e., does X minimize on costs while doing the job, or does X maximize what can be achieved given the costs?
Universal properties are system-level preferences embodied in the coordinating relationships among the members of the system. Universal properties say what it means for a mathematical object to be the best at a job, so they constitute a preference—you can totally order all candidates for the job by how well they do the job. And this preference doesn’t exist in any individual object but the system of relationships—3 isn’t the maximum of S because of anything about 3 but about how it relates to the other objects in S. These relationships, like functions, organize the system and tell the objects where to go, so they are the coordinating relationships. Virtual governors are system-level preferences embodied in the coordinating relationships among the members of the system, so universal properties are virtual governors.
Universal properties help the system maintain anatomical homeostasis. Say that A and B are each two-element sets, and AxB is the Cartesian product of A and B. Then suppose that A gets “damaged” and becomes a one-element set. The optimality test implied by the universal property of the Cartesian product then immediately recognizes that AxB is no longer optimal and identifies the class of objects that are. If the failure to pass the optimality test implies some pressure to move away from that role in the system, and if the ability to pass it implies some attraction to that role, then the system will naturally reorganize in response to damage to rediscover the optimal form.
Universal properties help the system maintain organizational allostasis. Allostasis basically means the set points of the system are flexible instead of rigid as in homeostasis. If you consider a totally ordered set with a maximum element, any object in that can serve as the maximum element just by putting it at the top of the order—the maximum element is relationally real, not assigned to one object as a special property of it. So the elements of a system can be rearranged if need be and maintain the universal property organizing the system.
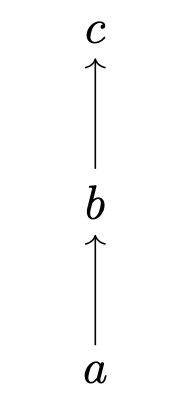
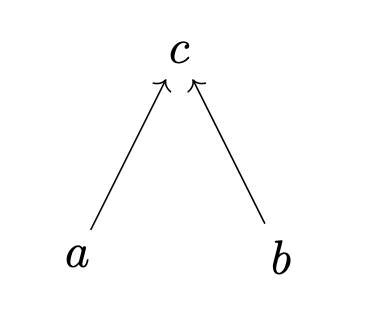
Universal properties help the system maintain behavioral allostasis. Here are two examples of ordered sets with maximum elements:
and
If you think of the arrows as legs, and move back and forth quickly between the two images, it looks like a body walking on two legs. if universal means system plan, then whole system following the plan while changing. But even though the forms are different, the system is always sticking to the group-level plan defined by the universal property indicated by the presence of a maximum element, c. So universal properties indicate a means by which a system can adjust its form to meet various challenges while maintaining a shared plan.
Universal properties embody the rule of law. A good governor maintains the rule of law, which means treating all members of the system indiscriminately. This condition is plainly achieved by universal properties, in which the universal object has a universal relationship with all other objects. For example, the maximum element in a set sees all other elements the same way, i.e., “I am bigger than you.”
Based on these considerations, I believe that all universal properties are virtual governors. Less obvious is the question of whether all virtual governors are universal properties. They may not be—for example, I think social interactions may engender virtual governors, and sometimes those virtual governors care very much the objects they’re looking at rather than maintaining the rule of law. But the connection between universal properties, a very abstract and mathematical concept, and physically observable virtual governors such as the price system, may provide some means of exploring how patterns from Platonic Space show up where we can see them.